目标检测--RetinaNet做数据部分

制作label，并计算loss。

首先理一下网络输出的shape，和数据label的shape。再看一下计算loss的时候应该怎么把数据转换成容易计算的形式。

1 shape

1.1 网络输出的shape

下图表示分类分支预测输出的feature map。格子表示featuremap上的像素。可以发现其实featuremap的每一层是预测种类别的信息，我们可以假设有四类别的信息，即x,y,w,h，当然实际预测的是x,y,w,h变换后的值。直接可以看出，每个4个像素对应一个anchor，且位置与原图上的位置相对应。

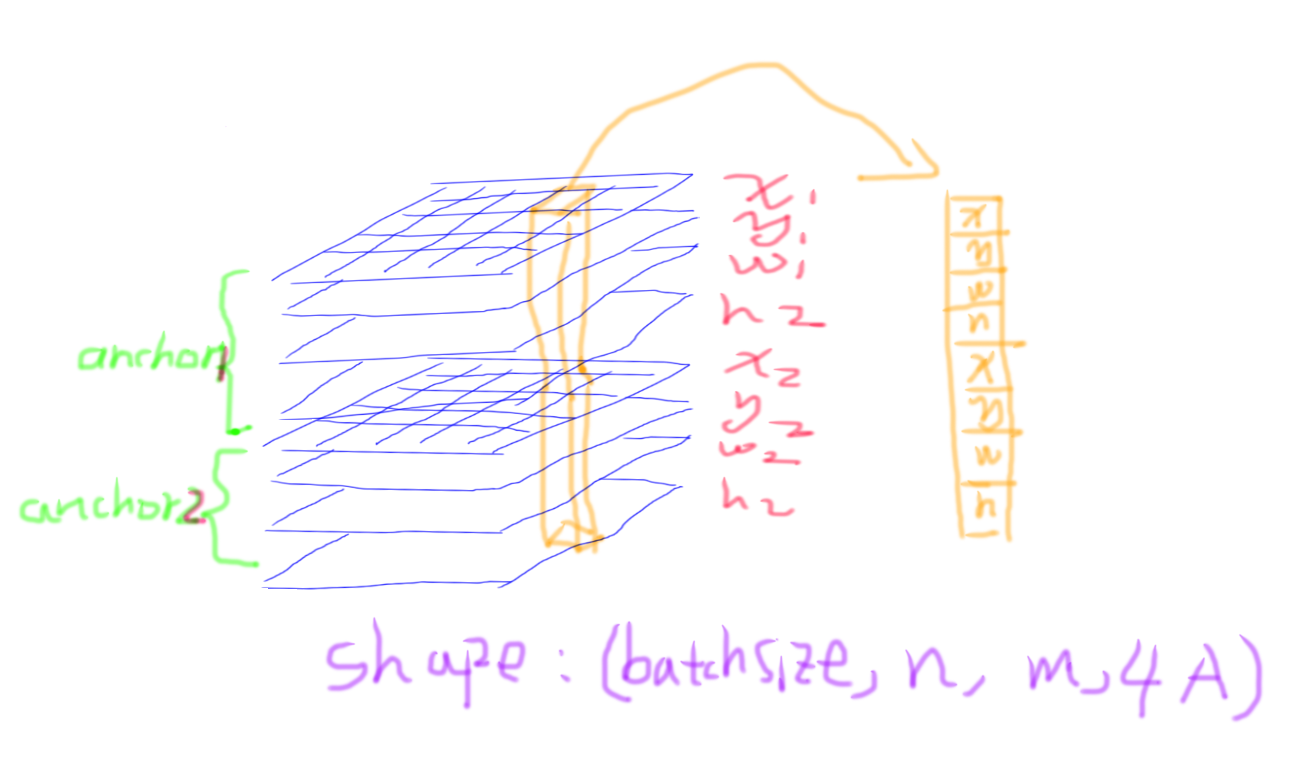
1.2计算loss时候的shape

因为我们需要计算fpn不同level层的损失（loss），由于不同level层的下采样次数不一样，所以featuremap的大小也不一样，这时候我们如果想要简单的将不同层的预测输出放在一个矩阵中，然后和label计算损失是不行的。因为像素宽度不一样，所以不能直接concat，所以我们需要reshape一下，再计算损失。reshape以后矩阵的每一行表示一个anchor。

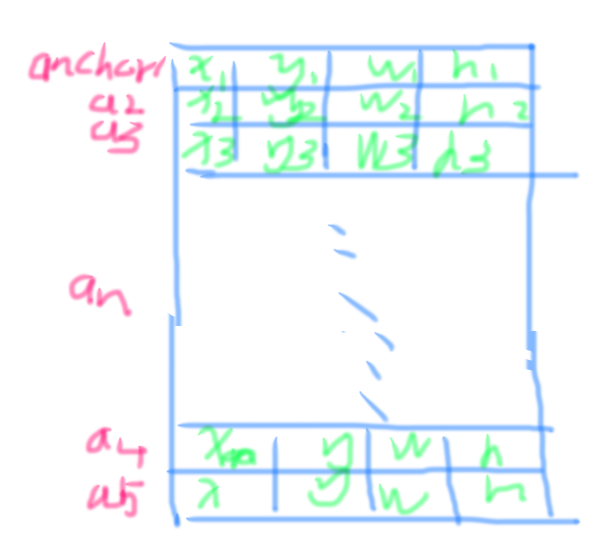
2 得到监督数据（label）或者说target

其实说起来很简单，就是对于每个anchor只分配一个与其iou最大的目标，注：这里不管目标是相同类别的还是不同类别的，都是取最大。

但是实现起来就比较复杂。首先考虑到有两种情况，同种类别击中一个anchor，或不同类别击中一个anchor。

看了别人代码(https://github.com/yhenon/pytorch-retinanet)以后才发现实现代码的时候一个代码就可以把这两种情况考虑进来。看起来没多少代码，但是感觉还是非常考验逻辑的。

2.1 高维度的广播机制，矩阵广播矩阵

首先用到了高纬度广播的机制。平时用的都是说把一个向量或是常量广播到矩阵或向量。
但是这里却把矩阵和矩阵进行广播。

简单的写一下广播的时候shape的变换：

（10, 4) + (2, 4) --对被加的矩阵扩展维度--> 
（10, 4, 1) + (2, 4) --> 
（10, 4, 1) + (2, 4) = (10, 4, 2)

其实可以看做把(2, 4)形状的矩阵的每一行拿出来和（10, 4)形状的矩阵相加，然后把两个结果concat起来。

2.2 数值索引和布尔索引的区别

False/true索引是只把true的索引出来。布尔索引要求shape要一致。
数值索引是把数值对应的数据拿出来然后堆叠到一起。数值索引不需要一致，且可以大于被索引的长度。

## 数值索引
In [58]: a = torch.randn(10,2)
Out[58]: 
tensor([[-0.6997,  0.6535],
        [-0.3947,  0.3171],
        [ 0.3076, -1.2978],
        [-0.4225, -0.3197],
        [-1.5714, -1.7430],
        [-0.2521,  0.6664],
        [ 0.6825, -1.2606],
        [-1.1892,  0.3615],
        [-0.3309, -0.0463],
        [ 0.2456, -0.0654]])

In [59]: IoU_max, IoU_argmax = torch.max(a, dim=1)

In [60]: IoU_max
Out[60]: 
tensor([ 0.6535,  0.3171,  0.3076, -0.3197, -1.5714,  0.6664,  0.6825,  0.3615,
        -0.0463,  0.2456])

In [61]: IoU_argmax
Out[61]: tensor([1, 1, 0, 1, 0, 1, 0, 1, 1, 0])

In [76]: bbox_annotation = np.array([[ 1,1,1,1],[2,2,2,2]])

In [77]: bbox_annotation[iou_argmax]
Out[77]: 
array([[2, 2, 2, 2],
       [2, 2, 2, 2],
       [1, 1, 1, 1],
       [2, 2, 2, 2],
       [1, 1, 1, 1],
       [2, 2, 2, 2],
       [1, 1, 1, 1],
       [2, 2, 2, 2],
       [2, 2, 2, 2],
       [1, 1, 1, 1]])

3 坐标回归

坐标回归的是相对anchor的一个偏移量（归一化偏移量）。

中心点回归：相对于anchor中心点的偏移，再除以anchor的宽度/高度。这里除以宽度相当于是做一个归一化，因为同样的偏移量但对于大目标和小目标的意义是不一样的。
宽/高回归：回归一个log（gt/anchor)；因为同样的宽高但对于大目标和小目标的意义是不一样的。大目标的宽高如果误差一点点我们希望提供的loss比较小，而小目标宽高如果误差一点点希望提供的loss比大目标的大一些。所以用log函数，因为log曲线的后面部分的值其实是比较小的，值的增长没那么快。
keras-retinanet中是回归左上角和右下角的角点坐标，回归的转换和中心点回归时候一样，只是对应的是anchor的角点，代码如下。

targets_dx1 = (gt_boxes[:, 0] - anchors[:, 0]) / anchor_widths
targets_dy1 = (gt_boxes[:, 1] - anchors[:, 1]) / anchor_heights
targets_dx2 = (gt_boxes[:, 2] - anchors[:, 2]) / anchor_widths
targets_dy2 = (gt_boxes[:, 3] - anchors[:, 3]) / anchor_heights

引用

https://github.com/yhenon/pytorch-retinanet
https://medium.com/@14prakash/the-intuition-behind-retinanet-eb636755607d

chuck